Introduction to Ripple Carry Adder
A Ripple Carry Adder is a digital circuit that performs the arithmetic operation of addition on binary numbers. It is one of the most basic and fundamental building blocks in digital electronics and computer architecture. The ripple carry adder gets its name from the way the carry bit “ripples” from one full adder to the next, starting from the least significant bit (LSB) to the most significant bit (MSB).
Binary Addition
Before diving into the details of ripple carry adders, let’s quickly review binary addition. In binary, there are only two digits: 0 and 1. When adding two single-bit numbers, there are four possible combinations:
| A | B | Sum | Carry |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
When the sum of two bits is 2 (1 + 1), the result is 0 with a carry of 1 to the next significant bit.
Full Adder
The core component of a ripple carry adder is the full adder. A full adder takes three inputs: two operand bits (A and B) and a carry-in bit (Cin), and produces two outputs: the sum (S) and a carry-out bit (Cout).
The truth table for a full adder is as follows:
| A | B | Cin | S | Cout |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
The Boolean expressions for the sum (S) and carry-out (Cout) are:
S = A ⊕ B ⊕ Cin
Cout = (A · B) + (Cin · (A ⊕ B))
where “⊕” represents the XOR operation, “·” represents the AND operation, and “+” represents the OR operation.
Half Adder
A full adder can be constructed using two half adders and an OR gate. A half adder takes two inputs (A and B) and produces two outputs: the sum (S) and a carry-out bit (Cout). The truth table for a half adder is:
| A | B | S | Cout |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
The Boolean expressions for the sum (S) and carry-out (Cout) in a half adder are:
S = A ⊕ B
Cout = A · B
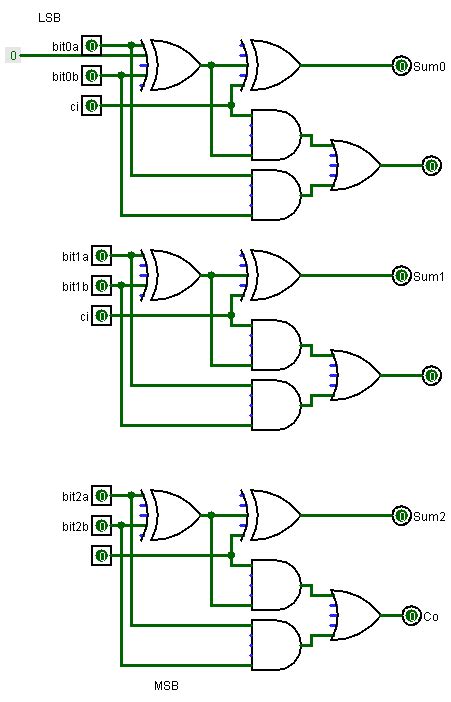
Ripple Carry Adder Construction
A ripple carry adder consists of multiple full adders connected in a chain, with the carry-out of each full adder connected to the carry-in of the next full adder. The number of full adders required depends on the number of bits in the operands.
For example, to add two 4-bit numbers, we need four full adders:
A3 B3 A2 B2 A1 B1 A0 B0
| | | | | | | |
v v v v v v v v
┌────┐ ┌────┐ ┌────┐ ┌────┐
│ FA │ │ FA │ │ FA │ │ FA │
└────┘ └────┘ └────┘ └────┘
| | | |
v v v v
C3 C2 C1 C0
The carry-out (Cout) of each full adder becomes the carry-in (Cin) of the next full adder. The carry-in of the least significant full adder is usually set to 0.

Ripple Carry Adder Operation
Let’s walk through an example of adding two 4-bit numbers using a ripple carry adder:
1 0 1 1 (A)
+ 0 1 0 1 (B)
───────
1 1 0 0 (Sum)
The addition process starts from the least significant bit (LSB) and propagates the carry to the next significant bit. Here’s how it works:
- LSB (Bit 0):
- A0 = 1, B0 = 1, Cin = 0
- S0 = 1 ⊕ 1 ⊕ 0 = 0
-
C1 = (1 · 1) + (0 · (1 ⊕ 1)) = 1
-
Bit 1:
- A1 = 1, B1 = 0, Cin = C1 = 1
- S1 = 1 ⊕ 0 ⊕ 1 = 0
-
C2 = (1 · 0) + (1 · (1 ⊕ 0)) = 1
-
Bit 2:
- A2 = 0, B2 = 1, Cin = C2 = 1
- S2 = 0 ⊕ 1 ⊕ 1 = 0
-
C3 = (0 · 1) + (1 · (0 ⊕ 1)) = 1
-
MSB (Bit 3):
- A3 = 1, B3 = 0, Cin = C3 = 1
- S3 = 1 ⊕ 0 ⊕ 1 = 0
- C4 = (1 · 0) + (1 · (1 ⊕ 0)) = 1
The final sum is 1100, and the carry-out (C4) is 1.
Propagation Delay in Ripple Carry Adders
One of the main drawbacks of ripple carry adders is the propagation delay. Since the carry bit needs to propagate from the LSB to the MSB, the time required for the addition operation depends on the number of bits in the operands.
The propagation delay in a ripple carry adder can be calculated as:
t_RCA = (n – 1) × t_FA + t_HA
where:
– t_RCA is the total propagation delay of the ripple carry adder
– n is the number of bits in the operands
– t_FA is the propagation delay of a single full adder
– t_HA is the propagation delay of the half adder in the LSB
As the number of bits increases, the propagation delay also increases linearly. This limits the speed at which ripple carry adders can perform addition on large numbers.
Alternatives to Ripple Carry Adders
Due to the propagation delay issue, ripple carry adders are not suitable for high-speed arithmetic operations on large numbers. Several alternative adder designs have been developed to improve the speed of addition:
Carry Lookahead Adder (CLA)
A Carry Lookahead Adder (CLA) is designed to reduce the propagation delay by calculating the carry bits in advance. It uses additional logic to determine the carry bits based on the input operands, allowing the addition to be performed more quickly.
Carry Select Adder (CSLA)
A Carry Select Adder (CSLA) divides the input operands into smaller groups and performs addition in parallel for each group, assuming both possible values of the carry-in (0 and 1). The correct sum is then selected based on the actual carry-in value.
Carry Skip Adder (CSA)
A Carry Skip Adder (CSA) divides the input operands into fixed-size blocks and uses additional logic to determine if the carry can skip a block, reducing the propagation delay.
These alternative adder designs offer faster performance compared to ripple carry adders, but they come with increased hardware complexity and cost.
Applications of Ripple Carry Adders
Despite their limitations, ripple carry adders are still widely used in various applications due to their simplicity and low hardware cost. Some common applications include:
- Arithmetic Logic Units (ALUs) in processors
- Digital signal processing (DSP) systems
- Embedded systems
- Calculator circuits
- Simple arithmetic operations in general-purpose digital circuits
Frequently Asked Questions (FAQ)
1. What is a ripple carry adder?
A ripple carry adder is a digital circuit that performs the arithmetic operation of addition on binary numbers. It consists of multiple full adders connected in a chain, with the carry-out of each full adder connected to the carry-in of the next full adder.
2. How does a ripple carry adder work?
A ripple carry adder works by adding two binary numbers bit by bit, starting from the least significant bit (LSB). The carry-out of each full adder is propagated to the carry-in of the next full adder, resulting in a “ripple” effect from the LSB to the most significant bit (MSB).
3. What is the main disadvantage of ripple carry adders?
The main disadvantage of ripple carry adders is the propagation delay. As the number of bits in the operands increases, the time required for the carry to propagate from the LSB to the MSB also increases linearly. This limits the speed at which ripple carry adders can perform addition on large numbers.
4. What are some alternatives to ripple carry adders?
Some alternatives to ripple carry adders include Carry Lookahead Adders (CLA), Carry Select Adders (CSLA), and Carry Skip Adders (CSA). These adder designs offer faster performance by reducing the propagation delay, but they come with increased hardware complexity and cost.
5. Where are ripple carry adders used?
Ripple carry adders are used in various applications where simple and low-cost arithmetic operations are required. They are commonly found in Arithmetic Logic Units (ALUs) of processors, digital signal processing (DSP) systems, embedded systems, calculator circuits, and simple arithmetic operations in general-purpose digital circuits.
Conclusion
Ripple carry adders are a fundamental building block in digital electronics and computer architecture. They perform the arithmetic operation of addition on binary numbers by propagating the carry from the least significant bit to the most significant bit. While ripple carry adders are simple and cost-effective, they suffer from propagation delay, which limits their performance for large operands.
Despite their limitations, ripple carry adders are still widely used in applications where low hardware cost and simplicity are prioritized over speed. For high-speed arithmetic operations, alternative adder designs like Carry Lookahead Adders, Carry Select Adders, and Carry Skip Adders are preferred, albeit at the cost of increased hardware complexity.
Understanding the principles and trade-offs of ripple carry adders is essential for anyone working with digital circuits and computer architecture. By mastering the concepts behind ripple carry adders, you can build a strong foundation for designing and analyzing more complex digital systems.





Leave a Reply