Introduction to Adders in Digital Electronics

In digital electronics, adders are essential components that perform the arithmetic operation of addition. They are fundamental building blocks in various digital circuits, including arithmetic logic units (ALUs), processors, and calculators. Adders come in different types, with the two most basic being the half adder and the full adder. Understanding the differences between these adders is crucial for designing efficient digital systems.

What is a Half Adder?

A half adder is a digital circuit that adds two single-bit binary numbers (A and B) and produces a sum (S) and a carry (C) as outputs. The half adder is the simplest form of an adder and is used when adding two bits without considering any carry input from a previous addition.

The truth table for a half adder is as follows:

A	B	S	C
0	0	0	0
0	1	1	0
1	0	1	0
1	1	0	1

The logic equations for a half adder are:
– Sum (S) = A ⊕ B (XOR)
– Carry (C) = A · B (AND)

Half Adder Circuit Diagram

A half adder can be implemented using an XOR gate for the sum and an AND gate for the carry. The circuit diagram for a half adder is shown below:

    A -----|XOR|-------- S
           |   |
    B -----|AND|-------- C

What is a Full Adder?

A full adder is a digital circuit that adds three single-bit binary numbers (A, B, and a carry-in, C_in) and produces a sum (S) and a carry-out (C_out) as outputs. The full adder is an extension of the half adder and is used when adding multiple bits, taking into account the carry from the previous addition.

The truth table for a full adder is as follows:

A	B	Cin	S	Cout
0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	0	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1

The logic equations for a full adder are:
– Sum (S) = A ⊕ B ⊕ C_in
– Carry-out (C_out) = (A · B) + (C_in · (A ⊕ B))

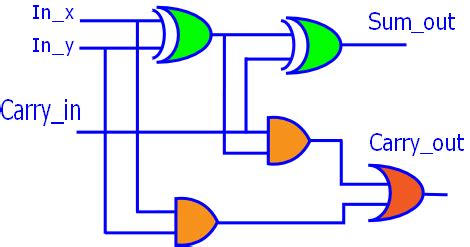
Full Adder Circuit Diagram

A full adder can be implemented using two half adders and an OR gate. The circuit diagram for a full adder is shown below:

          ┌─────┐
    A ----|     |
          | HA1 |---- S1 ---|
    B ----|     |           |    ┌─────┐
          └─────┘           |----|     |
             |                   | HA2 |---- S
             |              |----|     |
   C_in --------------------------└─────┘
                            |
                            |----- OR ---- C_out

Key Differences Between Half Adder and Full Adder

Number of Inputs

• Half Adder: A half adder has two inputs, A and B, which are the single-bit binary numbers to be added.
• Full Adder: A full adder has three inputs, A, B, and C_in. A and B are the single-bit binary numbers to be added, while C_in is the carry-in from the previous addition.

Number of Outputs

• Half Adder: A half adder has two outputs, sum (S) and carry (C).
• Full Adder: A full adder also has two outputs, sum (S) and carry-out (C_out).

Carry Handling

• Half Adder: A half adder does not have a carry-in input and cannot handle the carry from a previous addition. It is used for adding two single-bit numbers only.
• Full Adder: A full adder has a carry-in input, which allows it to handle the carry from a previous addition. This makes it suitable for adding multiple-bit numbers by cascading full adders.

Complexity

• Half Adder: A half adder is simpler in design and requires fewer gates (one XOR and one AND gate) compared to a full adder.
• Full Adder: A full adder is more complex and requires more gates (two half adders and one OR gate) to accommodate the carry-in input and generate the carry-out output.

Applications of Half Adders and Full Adders

Half Adder Applications

1. Single-bit addition: Half adders are used when adding two single-bit numbers without considering any carry from a previous addition.
2. Parity generators: Half adders can be used to generate parity bits for error detection in digital communication systems.
3. Multiplexers: Half adders can be used as building blocks in the design of multiplexers, which are digital circuits that select one of several input signals and forward it to the output.

Full Adder Applications

1. Multi-bit addition: Full adders are used to add multiple-bit numbers by cascading them together. Each full adder handles the addition of corresponding bits and the carry from the previous addition.
2. Arithmetic Logic Units (ALUs): Full adders are essential components in ALUs, which perform arithmetic and logical operations in processors.
3. Digital Signal Processing (DSP): Full adders are used in DSP applications, such as filtering and convolution, where high-speed addition is required.
4. Cryptography: Full adders are used in the implementation of various cryptographic algorithms, such as the Advanced Encryption Standard (AES) and the Secure Hash Algorithm (SHA).

Implementing Multi-bit Adders using Half Adders and Full Adders

To add multi-bit numbers, half adders and full adders can be cascaded together to form larger adder circuits. The choice between using half adders or full adders depends on the number of bits and the presence of carry-in from the previous addition.

Ripple Carry Adder

A ripple carry adder is a simple multi-bit adder that uses a series of full adders connected in a chain. The carry-out from each full adder is connected to the carry-in of the next full adder, allowing the carry to propagate through the circuit. The number of full adders required is equal to the number of bits in the input numbers.

The ripple carry adder is easy to design and implement but has a significant drawback in terms of propagation delay. As the carry propagates through each full adder, the delay accumulates, leading to slower overall performance, especially for larger bit-widths.

Carry Look-ahead Adder

To overcome the propagation delay issue in ripple carry adders, carry look-ahead adders (CLAs) were introduced. CLAs use additional logic to calculate the carry-in for each stage in advance, reducing the delay caused by the rippling of the carry.

In a CLA, the carry-in for each stage is determined by the propagate (P) and generate (G) signals, which are calculated based on the input bits. The propagate signal indicates whether a carry can be propagated through a stage, while the generate signal indicates whether a stage can generate a carry independently.

CLAs provide faster addition compared to ripple carry adders, especially for larger bit-widths. However, they require more complex hardware and have higher gate counts, which can increase the overall circuit area and power consumption.

Frequently Asked Questions (FAQ)

1. What is the main difference between a half adder and a full adder?
   The main difference between a half adder and a full adder is that a half adder does not have a carry-in input and cannot handle the carry from a previous addition, while a full adder has a carry-in input and can handle the carry from a previous addition.

2. Can a half adder be used to add multi-bit numbers?
   No, a half adder cannot be used alone to add multi-bit numbers because it does not have a carry-in input to handle the carry from the previous addition. To add multi-bit numbers, full adders are required.

3. What is the advantage of using a carry look-ahead adder over a ripple carry adder?
   The advantage of using a carry look-ahead adder over a ripple carry adder is that it reduces the propagation delay by calculating the carry-in for each stage in advance. This results in faster addition, especially for larger bit-widths.

4. How many gates are required to implement a half adder and a full adder?
   A half adder requires one XOR gate and one AND gate, while a full adder requires two half adders and one OR gate.

5. Can full adders be used in applications other than arithmetic operations?
   Yes, full adders can be used in various applications beyond arithmetic operations, such as in digital signal processing, cryptography, and error detection and correction circuits.

Conclusion

In digital electronics, half adders and full adders are the fundamental building blocks for performing binary addition. While half adders are simpler and used for adding two single-bit numbers, full adders are more complex and capable of handling carries from previous additions, making them suitable for adding multi-bit numbers.

Understanding the differences between half adders and full adders, as well as their applications, is crucial for designing efficient digital systems. By cascading these adders, designers can create multi-bit adder circuits like ripple carry adders and carry look-ahead adders to perform fast and reliable arithmetic operations in various digital applications.

As technology advances, the design and optimization of adder circuits continue to be an important area of research in digital electronics, aiming to improve performance, reduce power consumption, and minimize circuit area.