Introduction to Transistor Flip Flops

A transistor flip flop is a type of electronic circuit that is commonly used in digital systems to store and maintain binary data. It is a fundamental building block of sequential logic circuits, which are essential for creating memory elements, registers, and counters in digital circuits. Flip flops are capable of storing a single bit of information and can maintain their state even when the input signal is removed.

What is a Flip Flop?

A flip flop is a bistable multivibrator that has two stable states, typically referred to as the “set” and “reset” states. These states are represented by the output voltage levels, which are usually labeled as “high” (1) and “low” (0) in digital systems. The state of a flip flop can be changed by applying appropriate input signals, and the output will remain in that state until another input signal is applied to change it.

Types of Flip Flops

There are several types of flip flops, each with its own characteristics and functionality. The most common types are:

1. SR (Set-Reset) Flip Flop
2. D (Data) Flip Flop
3. JK Flip Flop
4. T (Toggle) Flip Flop

In this article, we will focus on the transistor-based implementation of these flip flops and their applications in digital circuits.

SR Flip Flop

The SR flip flop is the simplest type of flip flop and is the foundation for understanding the other types. It has two inputs, named “Set” (S) and “Reset” (R), and two outputs, labeled “Q” and “Q̄” (Q complement).

Truth Table

S	R	Q	Q̄
0	0	Q	Q̄
0	1	0	1
1	0	1	0
1	1	X	X

The truth table shows the behavior of the SR flip flop based on the input combinations. When both S and R are low (0), the flip flop maintains its previous state. If R is high (1) and S is low, the flip flop is reset, and the outputs become Q=0 and Q̄=1. If S is high and R is low, the flip flop is set, and the outputs become Q=1 and Q̄=0. The condition where both S and R are high is undefined and should be avoided, as it leads to an unstable state.

Transistor Implementation

The SR flip flop can be implemented using two cross-coupled NOR gates or two cross-coupled NAND gates. The NOR gate implementation is more common and is shown below:

[Insert a schematic diagram of the transistor-based SR flip flop using NOR gates]

In this implementation, the NOR gates are constructed using bipolar junction transistors (BJTs) or metal-oxide-semiconductor field-effect transistors (MOSFETs). The cross-coupling of the gates ensures that the flip flop maintains its state even when the inputs are removed.

D Flip Flop

The D flip flop, also known as the “data” or “delay” flip flop, is an extension of the SR flip flop that eliminates the undefined state when both inputs are high. It has a single data input (D) and two outputs (Q and Q̄).

Truth Table

D	Q	Q̄
0	0	1
1	1	0

The truth table shows that the output Q follows the input D, while Q̄ is always the complement of Q.

Transistor Implementation

The D flip flop can be implemented by modifying the SR flip flop circuit. One approach is to add an inverter to the S input and connect the data input (D) to both the S and R inputs, as shown below:

[Insert a schematic diagram of the transistor-based D flip flop]

This configuration ensures that the S and R inputs are always complementary, preventing the undefined state.

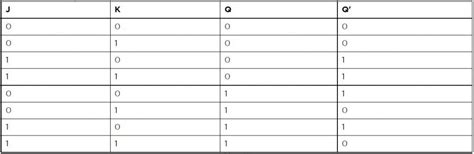
JK Flip Flop

The JK flip flop is a more versatile version of the SR flip flop that overcomes the limitation of the undefined state. It has two inputs, named “J” and “K,” and two outputs (Q and Q̄).

Truth Table

J	K	Q	Q̄
0	0	Q	Q̄
0	1	0	1
1	0	1	0
1	1	Q̄	Q

The truth table shows that when both J and K are low, the flip flop maintains its previous state. If K is high and J is low, the flip flop is reset (Q=0, Q̄=1). If J is high and K is low, the flip flop is set (Q=1, Q̄=0). When both J and K are high, the flip flop toggles its state, meaning that the outputs swap their values (Q becomes Q̄, and Q̄ becomes Q).

Transistor Implementation

The JK flip flop can be implemented using a modified SR flip flop circuit with additional logic gates. One common approach is to use two AND gates and two NOR gates, as shown below:

[Insert a schematic diagram of the transistor-based JK flip flop]

The AND gates are used to control the setting and resetting of the flip flop based on the J and K inputs, while the NOR gates form the basic SR flip flop structure.

T Flip Flop

The T flip flop, also known as the “toggle” flip flop, is a simplified version of the JK flip flop. It has a single input (T) and two outputs (Q and Q̄).

Truth Table

T	Q	Q̄
0	Q	Q̄
1	Q̄	Q

The truth table shows that when the T input is low, the flip flop maintains its previous state. When the T input is high, the flip flop toggles its state, meaning that the outputs swap their values (Q becomes Q̄, and Q̄ becomes Q).

Transistor Implementation

The T flip flop can be implemented by connecting the J and K inputs of a JK flip flop together and using the common input as the T input. The resulting circuit is shown below:

[Insert a schematic diagram of the transistor-based T flip flop]

This configuration ensures that the flip flop toggles its state whenever the T input is high.

Applications of Flip Flops

Flip flops are essential components in various digital systems and have numerous applications, such as:

1. Counters: Flip flops can be cascaded to create binary counters that keep track of the number of input pulses.

2. Shift Registers: Flip flops are used to store and shift binary data in shift registers, which are commonly used in serial communication and data processing.

3. Memory Elements: Flip flops serve as the basic storage elements in random-access memory (RAM) and other types of digital memory.

4. Finite State Machines: Flip flops are used to represent the states in finite state machines, which are used to control the behavior of digital systems based on input sequences.

5. Frequency Division: Flip flops can be used to divide the frequency of an input signal by a factor of two, which is useful in generating lower-frequency clock signals from a higher-frequency source.

Conclusion

Transistor flip flops are fundamental building blocks in sequential logic circuits and play a crucial role in storing and manipulating binary data in digital systems. By understanding the different types of flip flops, their truth tables, and their transistor-based implementations, designers can create complex digital circuits that perform various functions, such as counting, storing, and controlling the flow of data.

As technology advances, flip flops continue to evolve, with newer implementations using more advanced transistor technologies, such as CMOS (complementary metal-oxide-semiconductor), to improve performance, power efficiency, and integration density. Nonetheless, the basic principles and applications of flip flops remain essential for anyone working with digital electronics.

Frequently Asked Questions (FAQ)

1. What is the difference between a latch and a flip flop?
   A: A latch is a simple storage element that operates based on the level of the input signal, while a flip flop is a clocked storage element that changes its state only on the active edge of the clock signal.

2. Can a flip flop store more than one bit of information?
   A: No, a single flip flop can only store one bit of information. To store multiple bits, multiple flip flops must be used together.

3. What happens if both S and R inputs are high in an SR flip flop?
   A: When both S and R inputs are high in an SR flip flop, the output state is undefined and should be avoided. This condition is known as a “race” condition and can lead to unstable behavior.

4. What is the role of the clock signal in a flip flop?
   A: The clock signal is used to synchronize the operation of a flip flop. The flip flop changes its state only on the active edge (usually the rising edge) of the clock signal, ensuring that the output remains stable between clock transitions.

5. How can flip flops be used to create a binary counter?
   A: To create a binary counter, multiple flip flops are cascaded, with the output of one flip flop connected to the input of the next. The first flip flop toggles its state on each clock pulse, the second flip flop toggles its state on every second clock pulse, and so on, resulting in a binary count sequence.